Determining IIP3 of a DUT
[Proof of Identity:
1/2
∆ + Pi = IIP3 --using geometry]
Syed M. Ahmed
<<
return to library index
The
concept of Third-Order Intercept or IP3 in a gradual third-
and higher-order response, may be better grasped and the relationships and
definitions easily explained by rendering the problem to geometric representation as shown below.
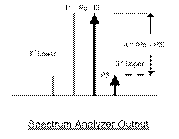
The IP3
measurement is performed by carefully‡ summing two frequency tones typically 1MHz apart and
sufficient (equal) power level, and applying to the input of the DUT. The DUT output
when viewed on a Spectrum Analyzer may look like the Fig:1 below. The
fundamental input tones at higher power flanked by third-order components usually at lower power
level. Since the input power Pi is known the Power Gain (G) may be determined,
one can then calculate the IIP3 using the well known identity:
1/2
∆ + Pi = IIP3; where ∆ = (Po - P3), and may be measured directly from the
Spectrum Analyzer.
‡‡ The details of setting up bench hardware are described in the
pdf version of this article and may be requested by e-mailing to the contact
below.
Proof of Identity:
1/2
∆ + Pi = IIP3 where ∆ = (Po - P3)
-- (1)
In
the above described setup, if the
input power to the DUT is increased gradually, for example in 1dB steps, then the
output tones rise at different rates. The 3rd order tone rising at 3x
the rate of the fundamental, which rises at 1x or 1dB, for every 1dB rise of
input power. The accompanying geometric figure captures this
principle, where
two right-triangles BAC and DAC, share a common side CA while the two
slopes corresponding to 1x and 3x are represented by their hypotenuse BA and DA.
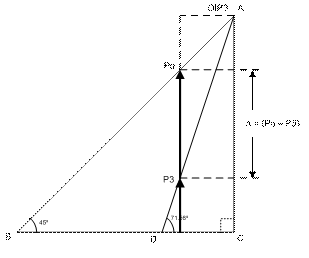
Applying the properties of right-triangles, in triangle BAC the hypotenuse
having slope 1x forces the sides BC and CA
to be equal and the corresponding angles to be 45º. The inner triangle DAC, the hypotenuse DA is constructed
with a slope 3x so that the other two sides DC and CA become fixed in that same ratio i.e.
side CA
is 3x of side DC, while the angle ADC is Tan-1 (AC/CD=3) or 71.56°. If the output power is depicted by a pair of vectors Po and P3
at an arbitrary distance past point D, then one can follow the outcome of gradual
rise of input power to the DUT; by pushing to the right and growing the vectors
Po and P3 at 1x and 3x rates until they both reach the same size and coincide
with side CA at the point A, or point C along the base. Point A represents the Output Third-Order Intercept
OIP3 which is a hypothetical point since
the DUT actually saturates well below the OIP3, slightly above it’s P1dB or gain
compression point.
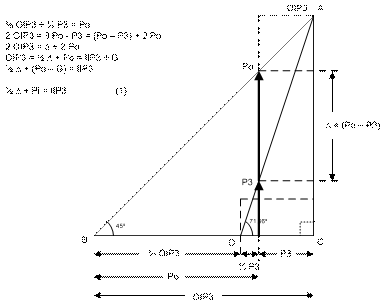
In the right-triangle formed by
side Po (the vector), hypotenuse PoB and the side BD extending up to the base of
Po; the starting expression may be written:
2/3
OIP3 +
1/3
P3 = Po (2)
Eventually, IIP3 or Input
Intercept Point the Input Power level that causes the output OIP3 is of
interest. IIP3 may be derived by subtracting the power Gain G from both sides of
the OIP3 expression --see steps below.
QED
<<
return to main page
A pdf version of above article
with more detail may be requested along with Questions and Comments by
e-mailing to the contact below :
AgileAccess™,
LLC
23 Londonderry Drive
Flemington, NJ
08822-1820
Ph:(908) 788-7740 ●
Fax:(908) 788-7746
e-mail:
contact@agileaccess.com


